- 제목: 사용자의 입력 의도를 반영한 음절 N-gram 기반 한국어 띄어쓰기 및 붙여쓰기 오류 교정 시스템
- 저널명: 한국정보과학회
- 출간년도: 2021
- 저자: 박서연(울산대학교), 옥철영(울산대학교)
- URL: https://www.dbpia.co.kr/Journal/articleDetail?nodeId=NODE10536782
요약
본 논문에서 말뭉치에서 음절 uni-gram, bi-gram, tri-gram의 빈도수를 계산하고 이를 활용하여 확률식을 학습하여 띄어쓰기 및 붙여쓰기 오류 교정 시스템을 구축한다. 딥러닝 모델을 사용할 경우 문장에 있는 띄어쓰기를 모두 제거하고 띄어쓰기를 교정하는데 본 논문은 원래 문장의 띄어쓰기를 반영하여 잘못된 띄어쓰기를 제거하고 띄어쓰기가 되지 않은 곳에 띄어쓰기를 제거한다. 딥러닝 모델보다 훨씬 가볍고 성능도 우수하다.
개요
- 한국어 자동 띄어쓰기란?
- 문장 내에서 어절 간의 경계를 예측하는 문제
- 띄어쓰기 오류의 문제점
- 문장 해석 어려움이 증가함
- 형태소 분석, 구문 분석, 개체명 인식과 같은 다음 단계의 자연어 처리의 오류를 발생시킴
관련 연구
- 규칙 기반 방식
- 문제점: 규칙 작성 및 유지가 힘듦
- 말뭉치 기반의 확률 및 통계 기반 방식
- 대규모의 말뭉치에서 음절 간의 띄어쓰기 확률 등의 정보를 활용하여 교정하는 방식
- [1] 임동희, 전영진, 김형준, 강승식.(2005).확장된 음절 bigram을 이용한 자동 띄어쓰기 시스템.한국정보과학회 언어공학연구회 학술발표 논문집,(),189-193.
- 기계학습 및 딥러닝 방법론
- 통계적 정보 이용
- 문제점: 기존 전통적인 방식을 사용한 띄어쓰기 시스템보다 속도가 느리고, 공백을 모두 삭제한 뒤 공백을 삽입하기 때문에 올바른 문장을 틀리게 수정하는 문제가 발생하기도 함
- [2] 이현영, 강승식.(2019).종단 간 심층 신경망을 이용한 한국어 문장 자동 띄어쓰기.정보처리학회논문지. 소프트웨어 및 데이터 공학,8(11),441-448.
- [3] 황현선, 이창기.(2016).딥러닝을 이용한 한국어 자동 띄어쓰기.한국정보과학회 학술발표논문집,(),738-740.
- [4] 황태욱, 정상근.(2019).BERT를 이용한 한국어 자동 띄어쓰기.한국정보과학회 학술발표논문집,(),374-376.
- [5] 이창기.(2014).사용자가 입력한 띄어쓰기 정보를 이용한 Structural SVM 기반 한국어 띄어쓰기.정보과학회논문지 : 컴퓨팅의 실제 및 레터,20(5),301-305.
제안 방안
- 음절 N-gram 통계 데이터 추출

- 문장에서 uni-gram, bi-gram, tri-gram의 좌우 공백이 나타나는 빈도를 계산함
- 이때 문장 시작과 끝은 띄어쓴다고 가정함
- 1은 공백 있음, 0은 공백 있음을 의미함
- n-gram별 띄어쓰기 유형 예시

- uni-gram에서는 4가지, bi-gram에서는 8가지, tri-gram에서는 16가지의 경우의 수가 있음
- '나', '나는', '나는학'이라는 uni-gram, bi-gram, tri-gram의 경우 각 n-gram의 띄어쓰기 유형은 위의 표에서 굵은 글씨에 해당함
- 공백 삽입 및 제거 확률 계산식 학습

- 위의 수식을 통해 bi-gram와 tri-gram 정보를 활용하여 uni-gram의 공백 삽입 및 제거 확률을 계산함
- 예시
$$P(학) = 0.46 \times P_{bi}(학) + 0.54 \times P_{tri}(학)$$
$$P_{bi}(학) = 0.3 \times P(는학○) + 0.375 \times P(학○교) + 0.325 \times P(○교에)$$
$$P_{tri}(학) = 0.22 × P(나는학○) + 0.27 × P(는학○교) + 0.27 × P(학○교에) + 0.24 × P(○교에간)$$ - bi-gram과 tri-gram의 확률을 구할 때 통계 정보를 활용하여 구할 수 있음
- 통계 정보를 활용한 n-gram 확률 계산 예시

- 하지만 모든 n-gram 확률을 추출한 통계 데이터로 계산할 수 없음
- uni-gram을 활용하여 간접적으로 bi-gram과 tri-gram의 확률을 계산함
- 연속된 음절 X, Y가 학습 데이터에서 한번도 등장하지 않은 경우
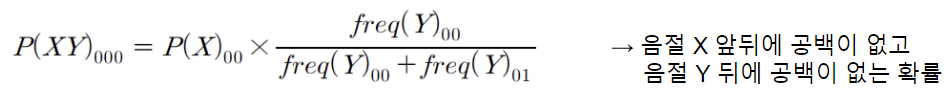
- 연속된 음절 X, Y, Z가 학습 데이터에서 한번도 등장하지 않은 경우
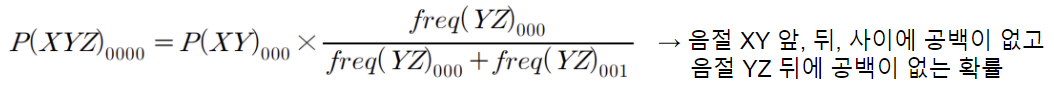
- 연속된 음절 X, Y가 학습 데이터에서 한번도 등장하지 않은 경우
- 각각의 가중치는 초기에는 1로 설정하고 학습 과정에서 각 식의 가중치의 합이 1이 되도록 조정하였음
- 가중치 조정 수식

- $ P(x_i) $의 가중치 $ w_0 $, $ w_1 $ 업데이트 예시
$$P(x_i) = w_0 \times P_{bi}(x_i) + w_1 \times P_{tri}(x_i)$$
$$w_0 = w_0 / (w_0 + w_1)$$
$$w_1 = w_1 / (w_0 + w_1)$$
- $ P(x_i) $의 가중치 $ w_0 $, $ w_1 $ 업데이트 예시
- 띄어쓰기 및 붙여쓰기 임계치 결정
- 확률 계산식 $P(x_i)$와 임계치(threshold)에 의해 공백 삽입 여부와 공백 제거 여부를 결정함
- 띄어쓰기 임계치 2가지, 붙여쓰기 임계지 2가지로 총 4가지를 사용함
- 기본 띄어쓰기 임계치: 한 어절이 5음절 미만일 때 사용됨
- 완화된 띄어쓰기 임계치: 한 어절이 5음절 이상일 때 사용됨
- 기본 붙여쓰기 임계치: 연속된 두 어절의 음절 수의 합이 3음절 초과일 때 사용됨
- 완화된 붙여쓰기 임계치: 연속된 두 어절의 음절 수의 합이 3음절 이하일 때 사용됨
- 띄어쓰기 및 붙여쓰기 교정
- 알고리즘

- 문장의 띄어쓰기 태그 추출
- 나는 학교에 간다. → 101001001
- tri-gram과 bi-gram의 확률 계산
- 학습된 확률 계산식과 간접적인 확률 계산식 사용
- 문장에서 잘못된 공백 제거
- 처음에는 threshold = 기본 붙여쓰기 임계치
- 이전 어절 길이 + 현재 어절 길이 <= 3 이면, threshold = 완환된 붙여쓰기 임계치
- uni-gram의 확률 계산 후 threshold보다 크면 어절 뒤에 존재하는 공백 제거
- 잘못된 공백이 제거된 문장에 올바른 공백 추가
- 처음에는 threshold = 기본 띄어쓰기 임계치
- 어절의 음절 개수 >= 5 이면, threshold = 완화된 띄어쓰기 임계치
- uni-gram의 확률 계산 후 threshold보다 크면 어절 뒤에 공백 추가
- 문장의 띄어쓰기 태그 추출
- 알고리즘
실험
- 학습 및 평가 데이터: 세종 말뭉치
문장 어절 학습 775,234 8,976,303 평가 86,138 998,182 - N-gram 기반 자동 띄어쓰기 시스템을 이용한 실험 결과
- 입력의 공백을 모두 제거한 후, 확률식이 임계칩다 크면 공백을 추가하는 방식과 비교한 결과
- 비교 결과 음절 단위 정확률 2.19%, 공백 F1 값 3.64%, 어절 F1 값 7.00%의 성능 개선이 됨

- 오류 문장 생성 예시
- 입력 문장에 띄어쓰기 및 붙여쓰기 오류가 포함되어 있을 경우의 성능 평가를 위해 임의로 오류 문장을 생성함

- 입력 문장에 띄어쓰기 및 붙여쓰기 오류가 포함되어 있을 경우의 성능 평가를 위해 임의로 오류 문장을 생성함
- 기존 한국어 자동 띄어쓰기 연구들과의 성능 비교
- 기존 연구들도 세종 말뭉치를 사용하였음
- 사용자의 입력 의도를 반영하지 않은 기존 연구들보다 더 높은 음절 정확률을 보임

- 네이버 영화 리뷰 말뭉치를 이용한 성능 평가
- 실제 사용자들의 영화평으로 성능 평가
- 모델 1은 세종 말뭉치만을 한습한 경우, 모델 2는 자동 띄어쓰기가 적용된 네이버 영화 리뷰 말뭉치의 학습 셋을 추가로 학습한 경우
- 공백 재현율은 81,07%지만, 공백 정밀도가 99.24%로 사용자가 띄어 써야 할 부분에서 띄어 쓰지 않는 경우가 많고, 실제로 띄어 쓴 부분은 충분히 신뢰할 수 있음
- 따라서 이를 반영하여 교정하는 것이 올바른 문장을 틀리게 수정하는 문제를 해결할 수 있다고 볼 수 있음

- [5]에서 초당 11.09 문장(316.89 음절)을 처리한 결과와 비교하면 제안방안은 초당 2691.69 문장(약 31,193,19 어절)을 처리하여 더 빠른 속도로 높은 성능을 낼 수 있음을 보여줌
'Study' 카테고리의 다른 글
| 분류 모델 성능 평가 지표(Accuracy, Precision, Recall, F1 score 등) (2) | 2022.01.02 |
|---|---|
| BM25 (0) | 2021.12.13 |
| TF-IDF(Term Frequency - Inverse Document Frequency) (0) | 2021.12.13 |
| DTM(Document-Term Matrix) (0) | 2021.12.13 |
| GLUE Benchmark (0) | 2021.11.07 |